લેખક: રાજેન્દ્ર દવે/ સી. એમ. નાગરાણી
લેખના પહેલા તેમજ બીજા ભાગમાં આપણે કક્ષા વિષેની એકાદ-બે વાતની ચર્ચા મુલતવી રાખી હતી. હવે, જ્યારે આપણે કક્ષા વિષેની પ્રાથમિક સમજ મેળવી લીધી છે, ત્યારે એને વધુ ટાળી શકાય એમ નથી.
અત્યાર સુધીની ચર્ચામાં આપણે ધારી લીધું કે કક્ષાની કોઇ પણ પ્રણાલી (System- સીસ્ટમ)માં હલકો પિંડ ભારે પિંડની આસપાસ કક્ષામાં ફરે છે, જ્યારે ભારે પિંડ કક્ષાના કેન્દ્ર (અથવા ફોકસ) પર સ્થિર હોય છે. પરંતુ આ કથન સાવ સાચું નથી. માત્ર જે પ્રણાલીમાં એક પિંડની સરખામણીમાં બીજા પિંડનું દળ (mass- માસ) – તેનું વજન- નગણ્ય હોય, ત્યાં સરળતા ખાતર આવી ધારણા કરી શકાય. જેમ કે, પૃથ્વીની કક્ષામાં ઘૂમતા સૌથી ભારે પિંડ ચંદ્રનું વજન પૃથ્વીના વજનના 1.2% જેટલું જ છે, અને સૂર્ય-મંડળના સૌથી વજનદાર ગ્રહ ગુરુ કરતા પણ સૂર્ય 1,000 ગણો વધુ ભારે છે. પરંતુ સમગ્ર બ્રહ્માંડ પર નજર નાખીએ તો એવા ઘણા અપવાદ જોવા મળે, જ્યાં આવી ધારણાને વાજબી ઠેરવવી મુશ્કેલ છે.

આવો એક અપવાદ તો આપણે નરી આંખે પણ જોઇ શકીએ છીએ. સપ્તર્ષિ તારામંડળમાં છઠ્ઠા ક્રમે જે બે તારા -વશિષ્ઠ (Mizar -મીઝાર) અને અરુંધતી (Alcor- આલ્કોર) – એકબીજાની ખૂબ નજીક જોવા મળે છે, તે એકબીજાની આસપાસ કક્ષામાં ઘુમી રહ્યા છે. વળી વશિષ્ઠ તારો અરુંધતી તારા કરતા માત્ર 1.2 ગણો જ ભારે છે. આકાશમાં સૌથી પ્રકાશિત દેખાતો તારો વ્યાધ (Sirius- સિરીયસ) પણ આવી એક દ્વિ-તારક (Binary star- બાયનરી સ્ટાર) પ્રણાલી છે, જેમાં ભારે તારો હલકા તારા કરતા માત્ર બે ગણો ભારે છે. આવી, લગભગ સરખા વજનના પિંડ વાળી પ્રણાલીમાં કયો પિંડ કેન્દ્રમાં હોય અને કયો કક્ષામાં? સાચી વાત તો એ છે કે પરસ્પરના ગુરુત્વાકર્ષણની અસર હેઠળ ગતિ કરતા કોઇ પણ બે પિંડ પૈકી બન્ને પિંડ, પ્રણાલીના ગુરુત્વકેન્દ્ર (Center of mass-સેન્ટર ઓફ માસ) , જેને પ્રણાલીનું બેરીસેન્ટર- Barycenter કહે છે, તેની આસપાસ કક્ષામાં ઘૂમે છે. બે પૈકી કોઇ પિંડ સ્થિર નથી હોતો. આ કથન સૂર્ય-પૃથ્વી, પૃથ્વી-ચંદ્ર, અને પૃથ્વી અને તેના કૃત્રિમ ઉપગ્રહ સહીતની દરેક પ્રણાલી માટે સાચું છે. પરંતુ જ્યાં એક પિંડ બીજા કરતાં અતિ ભારે હોય, ત્યાં બેરીસેન્ટર ભારે પિંડના કેન્દ્રની એટલું પાસે હોય કે બન્ને બિંદુ એક જ છે એમ માની શકાય. તેથી એમ માની શકાય કે ભારે પિંડ સ્થિર છે, અને માત્ર હલકો પિંડ કક્ષામાં ઘૂમે છે. ઉદાહરણ રૂપે, પૃથ્વી અને સૂર્ય વચ્ચેનું અંતર 15 કરોડ કિ.મી. છે જ્યારે પ્રણાલીનું બેરીસેન્ટર સૂર્યના પેટાળમાં, એના કેન્દ્રથી માત્ર 450 કિ.મી. દૂર છે. આમ, પૃથ્વી પોતાની 30 કરોડ કિ.મીની કક્ષામાં એક બાજુથી બીજી બાજુ જાય, ત્યારે સૂર્ય માત્ર 900 કિ.મી. હલે! (વાત હજુ વધારે જટિલ છે. સૂર્ય, ગ્રહો, ઉલ્કા, ધૂમકેતુ સહિત આખી સૂર્ય-મંડળ પ્રણાલીનું એક બેરીસેન્ટર બને. સૂર્ય અને પૃથ્વી બાકીના ગ્રહો, ઉલ્કા, ધૂમકેતુ સહિત સૂર્યમંડળના બધા પિંડ આની બેરીસેન્ટરની આસપાસની કક્ષામાં ફરે છે. પરંતુ હાલ પૂરતું ઉપરનું વિવરણ પર્યાપ્ત છે.)
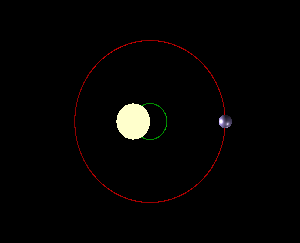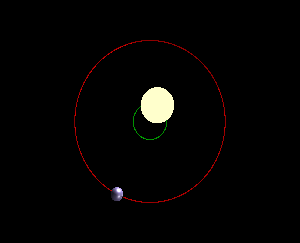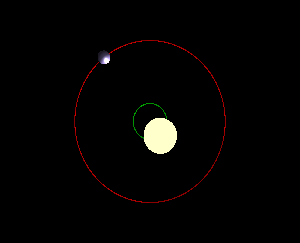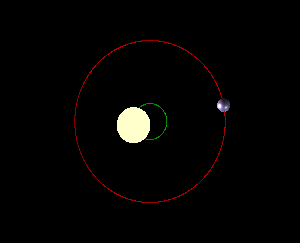
એક આડ-વાત. આપણે ઉપર જોયું એ પ્રમાણે પૃથ્વી- અને બીજા પિંડ- પોતાની કક્ષામાં ભ્રમણ કરે છે તે કારણે સૂર્યના સ્થાનમાં નાનો શો ફેરફાર થાય છે, એને પણ નાનકડી ગતિ મળે છે. આ હકીકત બીજા કોઇ પણ તારા માટે પણ સાચી છે. માટે, જો કોઇ તારાનું પોતાનું ગ્રહ-મંડળ હોય તો કક્ષામાં એમના ભ્રમણને કારણે પૃથ્વી પરથી જોતાં તારો આગળ-પાછળ જતો દેખાઈ શકે છે. બીજી રીતે કહીએ તો કોઇ પણ તારાની આગળ-પાછળની (રેડીઅલ- radial) ગતિ એની આસપાસ ફરતા ગ્રહોના અસ્તિત્વની ચાડી ખાય છે. સૂર્ય-મંડળની બહાર, બીજા તારાની આસપાસ ભ્રમણ કરતા બાહ્ય-ગ્રહ (Exoplanet – એક્ષોપ્લેનેટ)ની શોધ માટેની આ એક મહત્વની રીત છે, જેને રેડીઅલ વેલોસીટી -radial velocity રીત કહે છે.

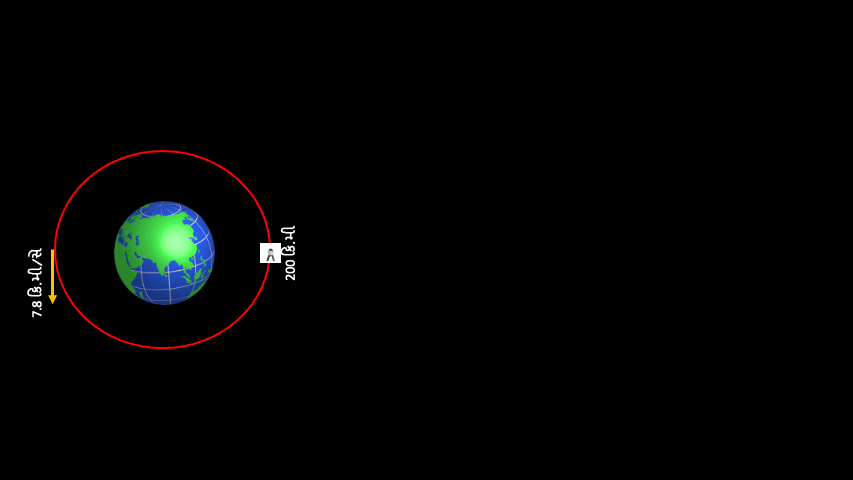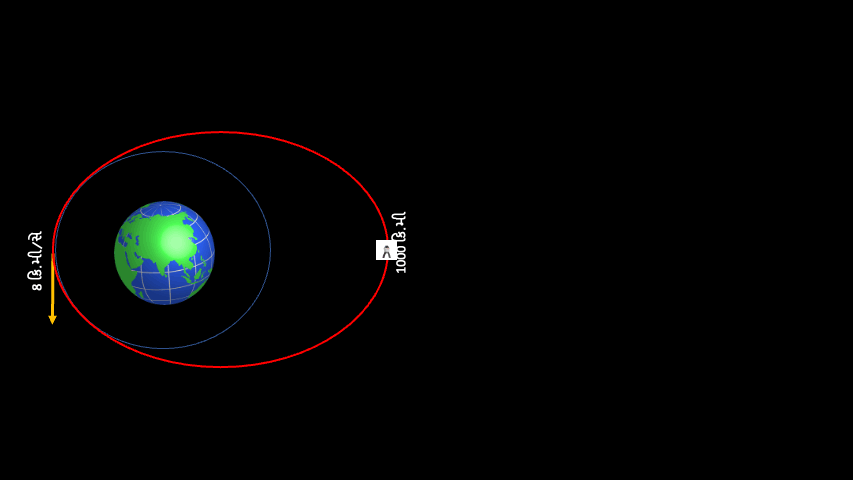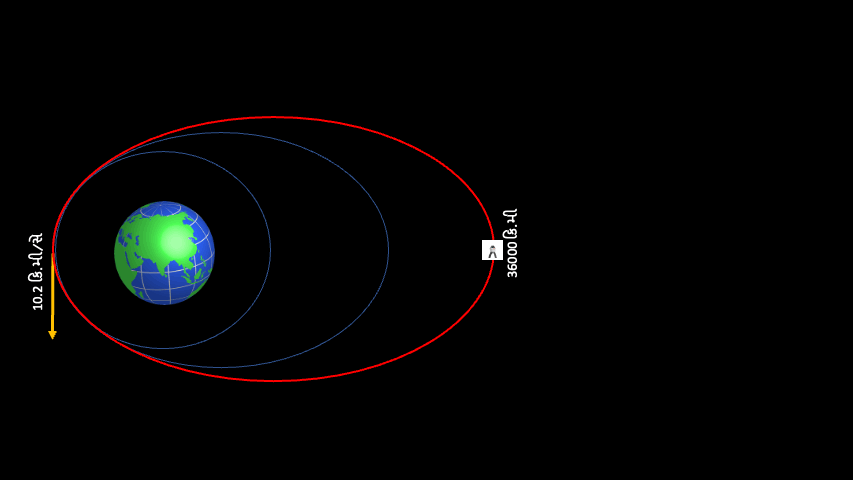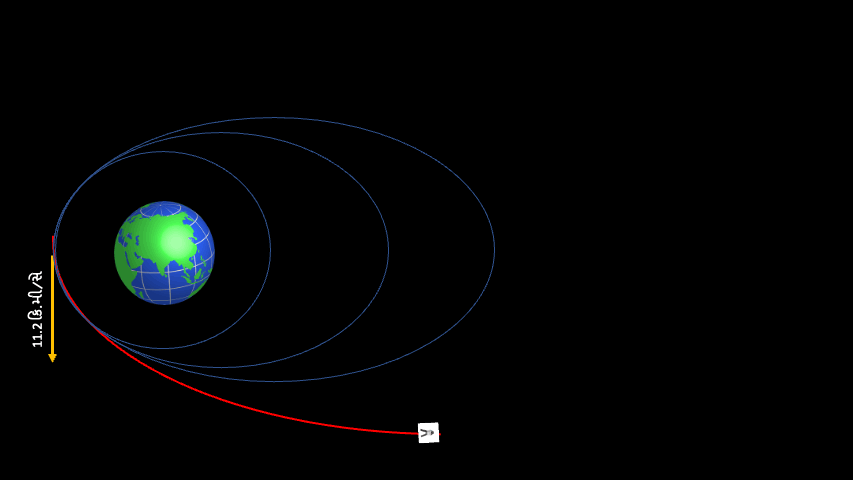
હવે આપણે જેની ચર્ચા મુલતવી રાખી હતી એવા બીજા વિષય પર આવીએ. લેખના પહેલાં ભાગ માં આપણે જોયું કે કક્ષામાં ભ્રમણ કરતા પિંડની ગતિ જો વર્તુળાકાર કક્ષા માટે જરૂરી ગતિ કરતાં વધુ હોય, તો કક્ષા લંબગોળ અથવા ઇલીપ્સ આકારની બને છે. ગતિ જેટલી વધુ, ઇલીપ્સ એટલો લાંબો. ઉદાહરણ રૂપે પૃથ્વીની સપાટીથી 200 કિ.મી ઉપર, વર્તુળાકાર કક્ષા માટે જરૂરી ગતિ આશરે 7.8 કિ.મી/સે. છે. આ ગતિ જો 8.0 કિ.મી./સે. હોય, તો કક્ષાની પેરીજી તો 200 કિ.મી જ રહેશે, પરંતુ કક્ષાના પૃથ્વીથી સૌથી દૂરના બિંદુ -એપોજી- ની ઊંચાઇ 1000 કિ.મી. થશે. 200 કિ.મી ઊંચાઇએ કક્ષામાં મૂકેલા યાનની એપોજી જો 36,000 કિ.મી જેટલી ઊંચે લઇ જવી હોય (36,000 કિ.મી. શા માટે? ઉત્તર માટે થોડી ધીરજ રાખો), તો તેના માટે 10.2 કિ.મી./સે. ગતિની જરૂર પડે. આવી રીતે યાનની ગતિ વધારતા જઇએ તો એક સમયે કક્ષાની એપોજીની ઊંચાઇ એટલી વધી જાય, કે યાન પૃથ્વી ભણી કદી પાછું આવે જ નહીં, માનો કક્ષાની એપોજી અનંત અંતરે પહોંચી ગઇ! આ સ્થિતિમાં યાનની કક્ષા, જે અત્યાર સુધી બધી બાજુથી બંધ એવા લંબગોળ -ઇલીપ્સ- આકારની હતી, તે એક બાજુથી ખુલ્લા એવા કોનિક સેક્શન પ્રકારના અન્ય વક્ર, પરવલય -પેરાબોલા- આકારની થઇ જાય.
બીજી રીતે વિચારતાં, યાનની ગતિ અને ગુરુત્વાકર્ષણ વચ્ચે રસ્સી-ખેંચની રમત જેવો એક પ્રકારનો ગજગ્રાહ ચાલે. એક તરફ યાનની ગતિ યાનને પૃથ્વીથી દૂર લઇ જવાનો પ્રયત્ન કરે, તો બીજી તરફ ગુરુત્વાકર્ષણ યાનને પૃથ્વી તરફ લાવવાનો પ્રયત્ન કરે. ગુરુત્વાકર્ષણને કારણે યાનની ગતિ ઘટતી તો જાય, પરંતુ ન્યુટનના ગુરુત્વાકર્ષણના નિયમ અનુસાર જેમ-જેમ યાનનું પૃથ્વીથી અંતર વધે, તેમ-તેમ ગુરુત્વાકર્ષણ પોતે પણ ઘટતું જાય. આ હરીફાઇના પરિણામનો આધાર કોણ પહેલા થાકી જાય એના પર છે. જો શરૂઆતની ગતિ ઓછી હોય તો, ગતિની કિંમત શૂન્ય કરી, તેની દિશા ઉલટાવી, યાનને પાછું વાળવામાં ગરુત્વાકર્ષણ સફળ રહે. પરંતુ શરૂઆતની ગતિ વધારે હોય, તો તે ઘટીને શૂન્ય થાય એ પહેલાં ગુરુત્વાકર્ષણ પોતે થાકી જાય!
જે ગતિ યાનને હંમેશ માટે પૃથ્વીથી દૂર લઇ જાય એવી પેરાબોલા આકારની ખુલ્લી કક્ષા બનાવે, તે ગતિને પૃથ્વી માટેની પલાયન-ગતિ (Escape Velocity- એસ્કેપ વેલોસીટી) કહે છે. આ ગતિની કિંમત પૃથ્વીના દળ (વજન) અને યાનને જે ઊંચાઈએથી કક્ષામાં મુકવામાં આવે તેના પર આધાર રાખે છે. પૃથ્વીની સપાટી પાસે પૃથ્વી માટેની એસ્કેપ વેલોસીટીની કિંમત આશરે 11.2 કિ.મી/સે. (40,320 કિ.મી/કલાક) છે.
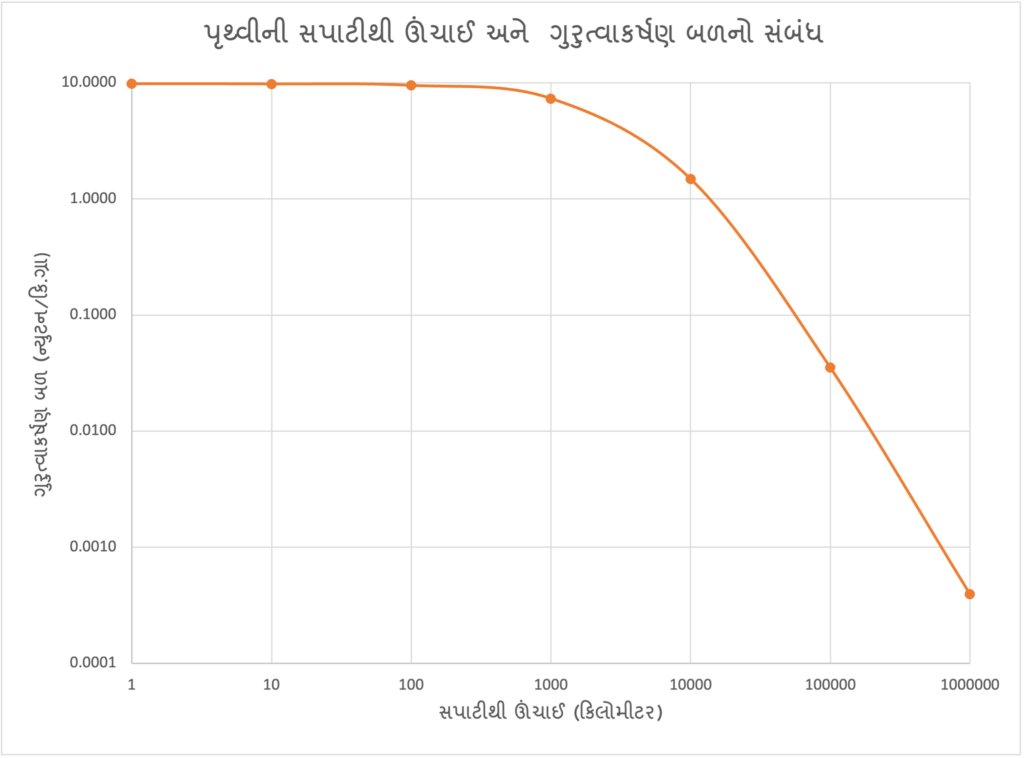
ઘણા મિત્રોએ કોઇ પુસ્તક અથવા લેખમાં વાંચ્યું હશે કે એસ્કેપ વેલોસીટી જેટલી ગતિ ધરાવતું યાન છેવટે પૃથ્વીના ગુરુત્વાકર્ષણની બહાર પહોંચી જાય. આ વિધાન સાવ ખોટું છે એમ તો કહી ન શકાય, પરંતુ એ પૂરેપૂરું યથાર્થ છે, એમ પણ ન કહી શકાય. ન્યુટનના ગુરુત્વાકર્ષણના નિયમ અનુસાર બે પિંડ વચ્ચે લાગતું ગુરુત્વાકર્ષણ બળ એમની વચ્ચેના અંતરના વર્ગના વ્યસ્ત પ્રમાણમાં હોય છે. આ નિયમ અનુસાર, દૂર જતા યાન પર પૃથ્વીના કારણે લાગતું ગુરુત્વાકર્ષણ બળ અંતર સાથે ઘટતું જરૂર જાય, પરંતુ તેની કિંમત શૂન્ય ક્યારે પણ ન થાય. આ અર્થમાં યાન ક્યારે પણ પૃથ્વીના ગુરુત્વાકર્ષણની “બહાર” ન નીકળી શકે.
બીજી તરફ, એસ્કેપ વેલોસીટીથી વધુ ગતિ ધરાવતા યાનને પૃથ્વીનું ગુરુત્વાકર્ષણ ક્યારે પણ પાછું પૃથ્વી ભણી ન વાળી શકે. છેવટે એક સમયે, પૃથ્વીથી દૂર જતા યાન પર પૃથ્વીના પ્રભાવ કરતા સૂર્યનો પ્રભાવ વધી જાય (. અહીં “પ્રભાવ” નો અર્થ માત્ર “ગુરુત્વાકર્ષણ બળ” નહીં પણ કાંઇક વિશેષ છે કેમ કે પૃથ્વી પોતાની સૂર્ય આસપાસની કક્ષામાં યાનને સાથે રાખીને ભ્રમણ કરે છે. માટે યાન પૃથ્વી તેમજ સૂર્ય બન્નેની કક્ષામાં ભ્રમણ કરે છે એમ માની શકાય પરંતુ એ જટિલ વિષયની વધુ ચર્ચા, લેખના સ્તરને ધ્યાનમાં લેતા અહીં અસ્થાને છે.) આ અર્થમાં યાન હવે પૃથ્વીના “ગુરુત્વાકર્ષણ”ની બહાર તો નહીં પણ તેના “પ્રભાવ ક્ષેત્ર” (Spere of Influence- સ્ફીઅર ઓફ ઇન્ફ્લુઅન્સ) ની બહાર જરૂર નીકળી જાય.
અલબત્, એસ્કેપ વેલોસીટી અને પેરાબોલિક કક્ષા વિષેની આ ચર્ચા માત્ર પૃથ્વી જ નહીં, પણ નાની ઉલ્કાથી શરૂ કરી મોટા તારા-વિશ્વ સમેત કોઇ પણ પિંડની આસપાસની કક્ષાને લાગુ પડે છે. અમેરિકાની અંતરિક્ષ સંસ્થા નાસાનું ઓસાયરીસ-રેક્ષ (OSIRIS-REx) યાન જે ઉલ્કા પરથી પથ્થરના નમૂના લઇ આવ્યું હતું તે બેનુ (Bennu) ઉલ્કા પરથી પલાયન થવા માટે પ્રતિ સેકન્ડ માત્ર 20 સેં.મી, અર્થાત્ કલાકના એક કિલોમીટરથી પણ ઓછી ગતિની જરૂર પડે, તો બીજી તરફ, સૂર્યની સપાટી પાસે રહેલા યાનને સૂર્ય-મંડળથી છટકવા માટે દર સેકન્ડે 600 કિ.મી. (21,60,000 કિ.મી./કલાક) થી પણ વધુ ગતિ જોઇએ! જેમ્સ વેબ ટેલિસ્કોપ જેવા, સૂર્યથી 15 કરોડ કિ.મી દૂર રહીને ભ્રમણ કરતા યાનને પણ સૂર્ય-મંડળથી છટકવા માટે 42 કિ.મી./સે (1,51,200 કિ.મી/કલાક) જેટલી ગતિ જોઇએ (સરખામણી રૂપે, અત્યારે એ યાન પ્રતિ સેકન્ડ 30 કિ.મી. ની ઝડપે સૂર્યની આસપાસ ફરી રહ્યું છે).
એક સ્વાભાવિક પ્રશ્ન: કક્ષામાં ભ્રમણ કરતા પિંડની ગતિ પલાયન ગતિ કરતા પણ વધુ હોય તો કક્ષાનો આકાર કેવો બને? એટલો જ સ્વાભાવિક ઉત્તર: જેવી રીતે વર્તુળાકાર ગતિથી વધુ ગતિ મળતા ઇલીપ્સ આકારની કક્ષા બને, કાંઇક એવી જ રીતે, એસ્કેપ વેલોસીટી કરતા વધારે ગતિ મળતા, કક્ષાનો આકાર પેરાબોલા કરતા પણ વધુ ખુલ્લા હાયપરબોલા વક્ર જેવો બને.
આ હતો કક્ષા-વિજ્ઞાનનો પ્રારંભિક પરિચય. આગળના કોઇક લેખમાં અંતરિક્ષ વિજ્ઞાન અને ટેકનોલોજી, તેમજ ખગોળશાસ્ત્રમાં વિવિધ પ્રકારની કક્ષાના ઉપયોગ અને ઉદાહરણ વિષે વાત કરીશું. ટિપ્પણી અને સૂચનનું હંમેશા સ્વાગત છે.