ઘણા સમય પહેલાં મેં આકાશ-દર્શનના જુદા-જુદા પાસા વિષે લખવાનું વચન આપ્યું હતું. એક યા બીજા કારણ સર હું આ વચન પાળી શક્યો નથી. જે હવે COVID-19ના ઓછાયા નીચે, નવરાશની પળોમાં પાળવાની કોશિશ કરી રહ્યો છું. કદાચ વાચક મિત્રો માટે પણ આ તણાવ સભર ફરજીયાત-ફૂરસદના સમયમાં આકાશ-દર્શન તેમનું ધ્યાન બીજી તરફ દોરવાનું એક ઉપયોગી સાધન બની શકે.
મારા આ પહેલાના લેખમાં દર્શાવ્યા મુજબ આકાશ-દર્શનનું પહેલું સોપાન, પહેલું પગથીયું તારા, ગ્રહ, અને નિહારિકા જેવા ખગોળીય- આકાશી પદાર્થ (Celestial Objects- સેલેસ્ટીયલ ઓબ્જેક્ટસ)નું આકાશમાં સ્થાન શી રીતે દર્શાવાય છે તે જાણવાનું છે. આપણે તે પણ જોયું હતું કે આકાશી નકશામાં પદાર્થનું સ્થાન દર્શાવાની પદ્ધતિ પૃથ્વી પરના સ્થળનું સ્થાન દર્શાવા માટે વપરાતી અક્ષાંશ-રેખાંશ પદ્ધતિની ખૂબ નજીક છે. અલબત, આ થોડી છેતરામણી ચીજ છે. પૃથ્વી પરનું સૌથી ઊંચું સ્થળ સમુદ્રની સપાટીથી આશરે 9 કિલોમીટર ઊંચે અને મહાસાગરનો સૌથી ઊંડો ભાગ તેની સપાટીથી આશરે 11 કિલોમીટર નીચે આવેલા છે. આ બેઉ અંતરનો તફાવત, 20 કિલોમીટર, પૃથ્વીની 6300 કિલોમિટર ત્રિજ્યાની સરખમણીમાં નગણ્ય છે માટે એમ કહી શકાય કે પૃથ્વી પરના સ્થળ લગભગએક સપાટી પર આવેલા છે. તેથી તેમનું પૃથ્વી પર સ્થાન બતાવવા માટે માત્ર બે પરિમાણ, બે Dimensions (ડાયમેન્શન્સ) પૂરતા છે. આ સામે આપણા સૌથી નજીકના ખગોળીય પદાર્થ ચંદ્ર અને અત્યાર સુધી જોવા મળેલા સૌથી દૂરના તારા- વિશ્વના અંતર વચ્ચે કરોડો પ્રકાશવર્ષનો ફરક છે. દેખીતું છે કે બધા ખગોળીય પદાર્થ એક જ સપાટી પર આવેલા છે તેમ માની શકાય નહીં, અને તેથી અંતરિક્ષમાં તેમના સ્થાનને દર્શાવા માટે અક્ષાંશ અને રેખાંશ જેવા બે પરિમાણ પૂરતા ન હોઇ શકે, તેમની સાથે ત્રીજું અંતરનું પરિમાણ ઉમેરવું પડે. આ મુંઝવણનો ઉકેલ લાવવા ખગોળશાસ્ત્રીઓએ પ્રાચીન પરંપરાની મદદ લીધી. પ્રાચીન ગ્રીસમાં એવી માન્યતા હતી કે બધાં તારા એક મોટા ગોળા પર ચોટાડેલા પ્રકાશિત બિંદુ છે. આ (કાલ્પનિક) ગોળાને આકાશી – કે દૈવી?- ગોળો, અર્થાત્ celestial sphere (સેલેસ્ટીઅલ સ્ફીઅર) કહે છે. આમ પણ કોઇ પણ પૃથ્વી પરના એક સ્થળેથી ટૂંકા સમય માટે જોતાં, બધાં ખગોળીય ખગોળિય પદાર્સથ સરખા અંતરે જ રહેલા હોય તેવો આભાસ થાય છે. આ આભાસને અવલોકન માટેના સીમિત ઉદ્દેશ માટે સ્વીકારી લેતાં માત્ર બે પરિમાણ આકાશી ગોળા પર સ્થિતિ દર્શાવા માટે પુરતા છે. આમ કંઇક અંશે આભાસી અને કંઇક અંશે ઐતિહાસિક કારણ સર આકાશી પદાર્થનું સ્થાન બે પરિમાણમાં બે યામ (coordinates- કોઓર્ડીનેટ્સ) વડે દર્શાવાનો રિવાજ છે.
આભાસી એવો આકાશી ગોળો પૃથ્વીનો સમ-કેન્દ્રી છે. અર્થાત્ તેનું કેન્દ્ર પણ પૃથ્વીના કેન્દ્ર પર જ સ્થિત છે. પૃથ્વીની પોતાની ધરી પર પશ્ચિમથી પૂર્વ દિશામાં ફરવાની ગતિને કારણે પથ્વીની સપાટી પરથી જોતાં આકાશી ગોળો, તેના પર લાગેલા તારા, સૂર્ય, ચંદ્ર, ગ્રહ તથા બીજા આકાશી પદાર્થ સાથે પૃથ્વીની આસપાસ દિવસમાં એક વખત પૂર્વથી પશ્ચિમ દિશામાં ફરતો દેખાય છે . આમ પૃથ્વીની ફરવાની ધરી, અને આપણા અકાશી-ગોળાની ફરવાની ધરી, બન્ને ઉત્તર-દક્ષિણ દિશામાં છે.
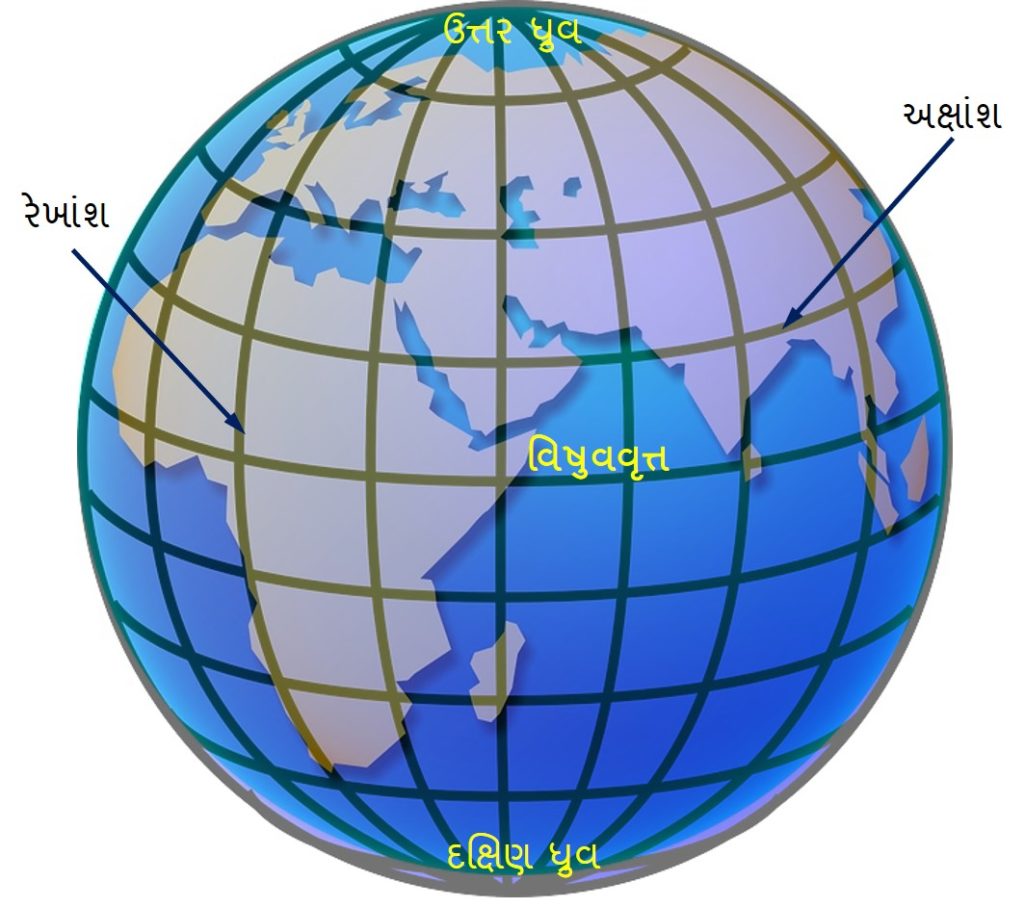
પૃથ્વી અને આકાશી-ગોળા, બન્ને પર સ્થાન દર્શાવવા માટે બે પરિમાણની જરૂર પડે અને તે બન્નેની મુખ્ય ધરી એક જ દિશામાં છે. તેથી સાહજિક છે કે બન્ને ગોળા પર સ્થાન દર્શાવાની પદ્ધતિ એકબીજાને મળતી હોય. પૃથ્વી ઉપર કોઇ પણ સ્થળની ઉત્તર-દક્ષિણ સ્થિતિ સ્થળના અક્ષાંશ દ્વારા દર્શાવાય છે અને પૂર્વ-પશ્ચિમ રેખાંશ દ્વારા. સમાન અક્ષાંશની (અલબત, આભાસી) રેખા પૃથ્વીના ગોળા પર વિષુવવૃત્તને સમાંતર વર્તુળ રૂપે હોય છે જ્યારે સમાન રેખાંશની (ફરી, આભાસી) રેખા બન્ને ધ્રુવમાંથી પસાર થતાં અર્ધ-વર્તુળ રૂપે હોય છે.
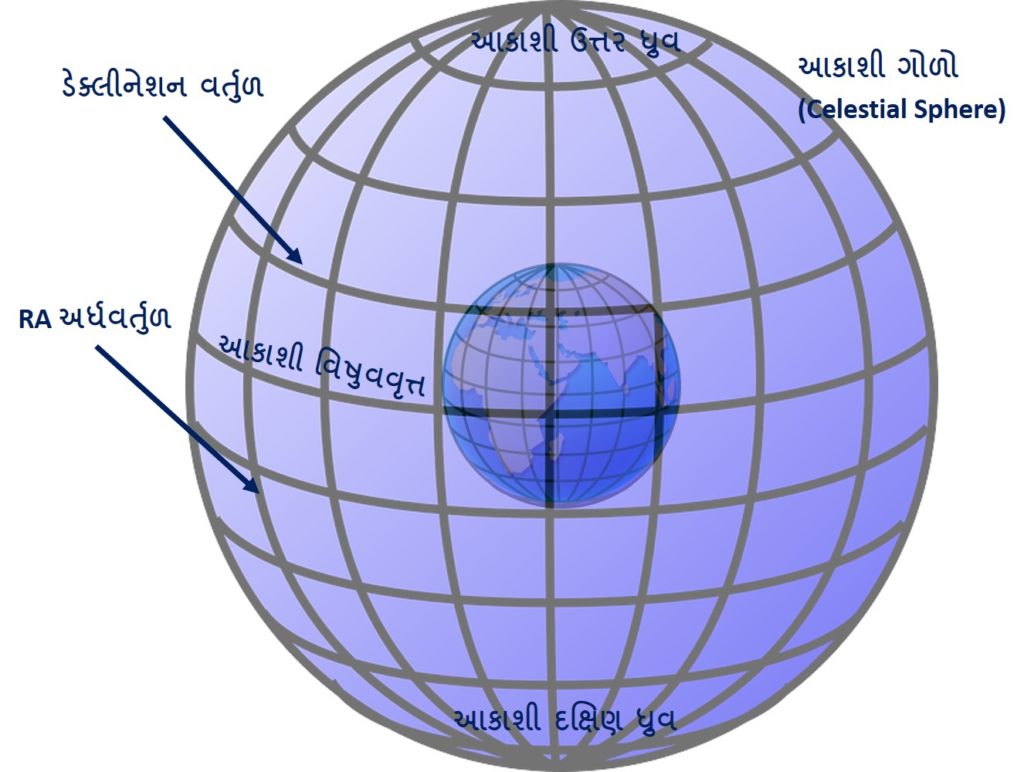
આકાશ-દર્શન વિષેના લેખમાં મેં સ્કાય-એન્ડ-ટેલિસ્કોપ સમાયિકનો ઉલ્લેખ કર્યો હતો. આ સામાયિકની વેબસાઇટ પરના લેખમાં અક્ષાંશ-રેખાંશને આકાશી ગોળા સુધી લઇ જવા માટે એક સુંદર કલ્પના કરી છે. માની લઇએ કે પૃથ્વી એક હવા ભરીને ફુલાવી શકાય તેવો દડો છે અને તેના પર અક્ષાંશ તથા રેખાંશની રેખા દોરેલી છે. હવે આ દડામાં આપણે એટલી હવા ભરીએ કે તે ફુલીને આકાશી ગોળા જેવડો થઇ જાય, તો તેના પર દોરેલી અક્ષાંશ અને રેખાંશની રેખા નો ઉપયોગ આકાશી ગોળા પર આકાશી પદાર્થનું સ્થાન દર્શાવવા કરી શકાય. આ પ્રણાલી (System-સિસ્ટમ) પ્રમાણે પૃથ્વીની સપાટી પરના વિષુવવૃત્તની બરોબર ઉપર, આકાશી ગોળા પર આકાશી વિષુવવૃત્ત (celestial equator- સેલેસ્ટીઅલ ઇક્વેટોર) છે અને પૃથ્વીના ઉત્તર અને દક્ષિણ ધ્રુવની બરોબર ઉપર આકાશી ઉત્તર અને દક્ષિણ ધ્રુવ (celestial pole- સેલેસ્ટીઅલ પોલ) આવેલા છે.
આપણે આગળ જોયું તે પ્રમાણે, પૃથ્વીની પોતાની ધરી પર પશ્ચિમથી પૂર્વ દિશા તરફ ફરવાની દૈનિક ગતિને કારણે આકાશી ગોળો આ બે આકાશી ધ્રુવમાંથી પસાર થતી ધરી પર પૂર્વથી પશ્ચિમ તરફ દિવસમાં એક વખત ફરતો દેખાય છે. આકાશી વિષુવવૃત્ત તથા આકાશી ધ્રુવની વચ્ચે પૃથ્વી પરના અક્ષાંશ માફક ડેક્લીનેશન -Declination વર્તુળ ( “ડેક્લીનેશન” નો સંસ્કૃત પર્યાય કદાચ “વિષુવાલમ્બ” છે. પરંતુ આ લેખમાં હું વધુ પ્રચલિત “ડેક્લીનેશન” જ વાપરીશ) આકાશી પદાર્થની ઉત્તર-દક્ષિણ સ્થિતિ બતાવે છે. અક્ષાંશની માફક ડેક્લીનેશન પણ અંશમાં મપાય છે. આકાશી વિષુવવૃત્ત પર આવેલા પદાર્થનું ડેક્લીનેશન 0 અંશ તો ધ્રુવ પર આવેલા પદાર્થનું 90 અંશ હશે. આકાશી વિષુવવૃત્તની ઉત્તરમાં આવેલા પદાર્થનું ડેક્લીનેશન ધન (+) અને તેની દક્ષિણમાં આવેલા પદાર્થનું ડેક્લીનેશન ઋણ (-) ગણાય છે. આમ ઉત્તર ધ્રુવની નજીક આવેલા ધ્રુવ તારકનું ડેક્લીનેશન લગભગ +89o16’ અર્થાત્ ધન 89 અંશ 16 કળા છે જ્યારે પૃથ્વીથી દેખાતો સૌથી પ્રકાશિત તારો વ્યાધ વિષુવવૃત્તથી દક્ષિણે લગભગ 16 અંશ 43 કળા પર છે. તેથી તેનું ડેક્લીનેશન આશરે -16o43’ છે.
પૃથ્વી પરના રેખાંશની સમકક્ષ આકાશી ગોળા પર પૂર્વ-પશ્ચિમ સ્થિતી દર્શાવા “રાઇટ એસેન્શન” – Right Ascension, ટુંકમાં RA વપરાય છે ( “રાઇટ એસેન્શન” નો સંસ્કૃત પર્યાય કદાચ “વિષુવાંશ” છે. પરંતુ આ લેખમાં હું વધુ પ્રચલિત “RA” જ વાપરીશ). રેખાંશની માફક સમાન RA ના અર્ધ-વર્તુળ (આકાશી) ધ્રુવમાંથી પસાર થાય છે. આકાશી ગોળો પૃથ્વીની આસપાસ એક ઘડિયાળની (12 નહીં, પણ 24 કલાક વાળી) માફક દિવસમાં એક વાર ફરતો દેખાય છે. તેથી તેને 24 RAમાં વિભાજિત કરેલો છે અને તેથી RA અંશ વડે નહીં પરંતુ કલાક , મિનિટ અને સેકન્ડ (Hour- h, minute- m second-s) વડે દર્શાવાનો રિવાજ છે. ઘડિયાળના સમયની માફક RA ની કિંમત પણ 0 h 0 m 0 s થી શરૂ કરી 23 h 59 m 59 s સુધીની હોઇ શકે. અલબત, આપણે કલાકમાં દર્શાવેલ RAને અંશમાં સહેલાઈ બદલી શકીએ. આખા દિવસમાં 360 અંશ ફરતા ગોળામાં RAના 24 કલાક રહેલા છે. તેથી એક કલાક RAમાં 15 અંશ હોય.
બે ધ્રુવની બરાબર મધ્યમાં રહેલું વિષુવવૃત્ત 0 અંશ અક્ષાંશ માટેનું કુદરતી વર્તુળ છે. પૃથ્વી પર રેખાંશની કોઇ એવી રેખા નથી જેને વિષુવવૃત્તની માફક કુદરતી રીતે 0 રેખાંશ કહી શકાય. કંઇક અંશે મનસ્વી કહી શકાય તેવી રીતે આપણે ઈંગ્લેન્ડમાં આવેલી ગ્રીનીચ- Greenwich વેધશાળાના રેખાંશને 0 અંશ રેખાંશ માની લીધા. આકાશી ગોળા માટે પરિસ્થિતિ તેટલી ખરાબ નથી. તેના પર એવા ખાસ RA અર્ધ-વર્તુળ છે, જેને 0 RA તરીકે લઇ શકાય. આપણે જાણીએ છીએ કે પૃથ્વીની ધરી, તેની કક્ષા સાથે કાટખૂણો નહીં બનાવતા 66.6 અંશનો ખૂણો બનાવે છે. બીજા શબ્દમાં કહીએ તો પૃથ્વીની ધરી અને કક્ષાના લંબ વચ્ચે 23.5 અંશનો ખૂણો બને છે. પરિણામ સ્વરૂપે, આકાશી વિષુવવૃત્ત અને પૃથ્વીની કક્ષા (ક્રાંતિવૃત્ત- અંગ્રેજીમાં Ecliptic- ઇક્લીપ્ટિક) વચ્ચે પણ 23.5 અંશનો ખૂણો બને અને તેઓ બન્ને એકબીજાને બે બિંદુ પર છેદે. આ બે બિંદુને સંપાત (Equinox- ઇક્વીનોક્ષ) કહે છે.
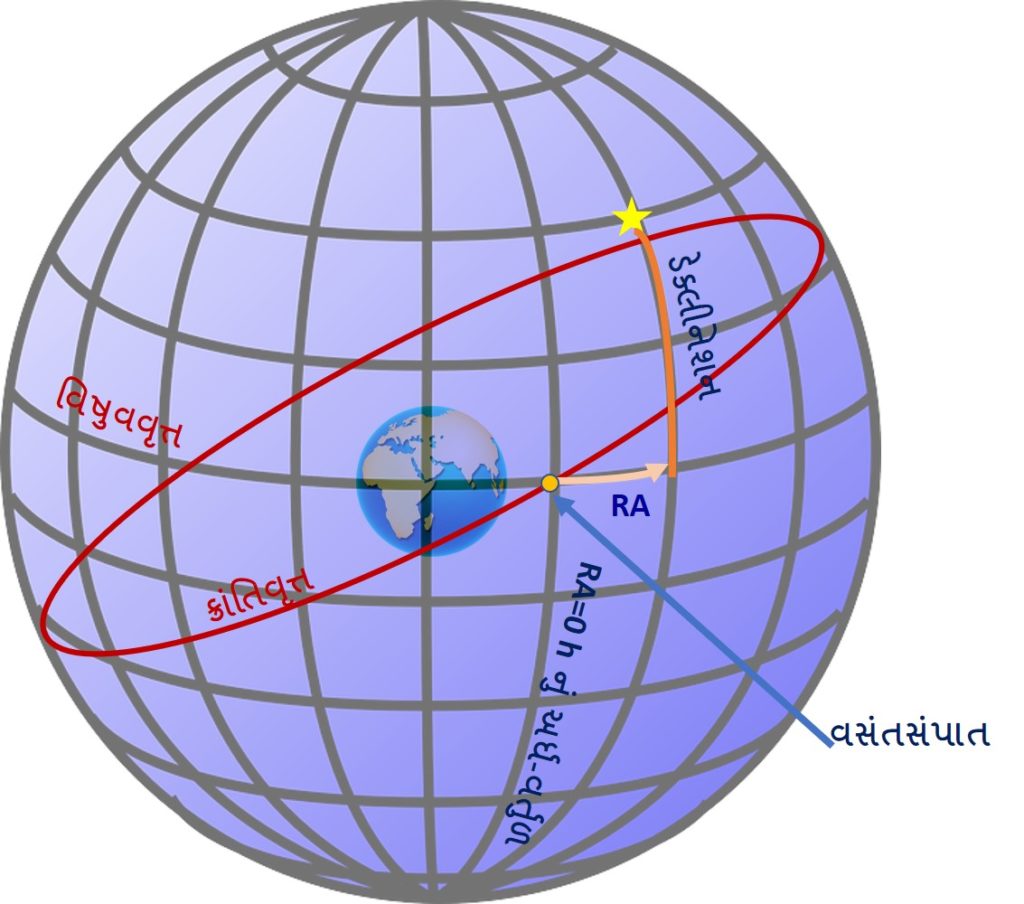
હવે પૃથ્વી પરથી જોતાં પૃથ્વી નહીં પણ સૂર્ય આ કક્ષામાં ભ્રમણ કરતો દેખાય છે. અર્થાત્ દૂર રહેલા તારાની પૃષ્ઠભૂમિ પર સૂર્ય વર્ષમાં એકવાર પરિભ્રમણ કરતો દેખાય છે. આ પરિભ્રમણ દરમ્યાન સૂર્ય 6 માસ માટે કક્ષાના એવા ભાગમાં દેખાય જે વિષુવવૃત્તથી ઉત્તરમાં છે તો બાકીના 6 માસ વિષુવવૃત્તથી દક્ષિણમાં. અને વર્ષમાં બે વખત તે બરોબર વિષુવવૃત્ત પર દેખાય, એક વખત દક્ષિણથી ઉત્તર તરફ જતાં અને 6 માસ બાદ ઉત્તરથી દક્ષિણ તરફ જતાં. પહેલા સંપાત વખતે- તારીખ 20 માર્ચની આસપાસ- ઉત્તર ગોળાર્ધમાં વસંત હોવાથી તેને વસંત સંપાત (Spring Equinox- સ્પ્રીંગ ઇક્વીનોક્ષ) કહે છે. તેવી જ રીતે બીજા સંપાત વખતે – તારીખ 23 સપ્ટેમ્બરની આસપાસ- શરદ ઋતુ હોવાથી તેને શરદ સંપાત (Autumnal Equinox- ઓટમનલ ઇક્વીનોક્ષ) કહે છે. આ બે સંપાત 0 h RA માટેના કુદરતી દાવાદાર છે. માનવજાત ઘણા ભાગે ઉત્તર ગોળાર્ધમાં વસે છે તેથી તેના માટે દક્ષિણમાંથી ઉત્તર તરફ જતા સૂર્યનું મહત્વ સ્વાભાવિક રૂપે વધુ હોય. કદાચ તેથી જ વસંત સંપાતમાંથી પસાર થતા RA અર્ધવર્તુળને 0 h RA ગણવામાં આવે છે ( જ્યાં સુધી હું જાણું છું, આપણા ભારતીય ખગોળ વિજ્ઞાનમાં પણ રાશી ચક્રની શરૂઆત મૂળભૂત રીતે વસંત સંપાતથી જ થતી હશે – આપણે આગળના લેખમાં જોઈશું તેમ વસંત સંપાત તારાના સંદર્ભમાં ખસતો રહે છે. તેથી આપણું રાશી ચક્ર અત્યારે વસંત સંપાતથી શરૂ નથી થતું).
આકાશમાં RA પશ્ચિમથી પૂર્વ તરફ વધતો જાય છે. તેથી મૃગશિર્ષમાં રહેલા તારા આદ્રાનો RA (5h 55m 10s) તેનાથી પૂર્વમાં દેખાતા તારા સ્વાતિના RA (14h 15m 41s) કરતા ઓછો છે. કેટલાક જાણીતા તારા અને બીજા આકાશી પદાર્થના RA અને ડેક્લીનેશન આ પ્રમાણે છે.
| નામ | અંગ્રેજી નામ | RA | ડેક્લીનેશન |
| દેવયાની તારાવિશ્વ | Andromeda Galaxy | 00h 42m 44s | +41o 16′ 09″ |
| કૃતિકા | Pleiades (M45) | 3h 47m | +24o 07′ |
| આદ્રા | Betelgeuse | 5h 55m 10s | +07o 24′ 25′ |
| મૃગશિર્ષ નિહારિકા | Great Orion Nebula (M42) | 5h 35m 17s | -05o 23′ 28″ |
| વ્યાધ | Sirius | 6h 45m 9s | -16o 42′ 58″ |
| અગત્સ્ય | Canopus | 6h 53m 27s | -52o 41′ 44″ |
| વશિષ્ઠ | Mizar | 13h 23m 27s | +54o 55′ 31″ |
| સ્વાતિ | Arcturus | 14h 15m 40s | +19o 10′ 57″ |
| અભિજિત | Vega | 18h 36m 56s | +38o 47′ 01″ |
| શ્રવણ | Altair | 19h 50m 47s | +08o 52′ 06″ |
| હંસપૂચ્છ | Deneb | 20h 41m 26s | +45o 16′ 49″ |
પ્રશ્ન એ ઊપજે કે જો દૂરના તારાના સંદર્ભમાં સંપાત ખસતા રહેતા હોય તો ઉપર દર્શાવેલ RA તથા ડેક્લીનેશન સંપાતની કઇ સ્થિતિ માટે સાચા છે? ખગોળશાસ્ત્રી લગભગ દર 50 વર્ષે સંપાતની સ્થિતિ નક્કી કરી તેના સંદર્ભમાં આકાશી પદાર્થના RA તથા ડેક્લીનેશનની ફેર ગણતરી કરે છે. ઉપર દર્શાવેલ યામ માટે સન 2000ની પહેલી જાન્યુઆરી સમયની સંપાતની સ્થિતિનો આધાર લેવાયો છે.
આ તો વાત થઇ નકશામાં આકાશી પદાર્થનું સ્થાન દર્શાવાની પદ્ધતિની. યામની આ પદ્ધતિને વિષુવવૃત્તિય (Equatorial- ઇક્વેટોરીઅલ) પદ્ધતિ કહે છે. આ પદ્ધતિની કેટલીક ખાસિયતની – જેમકે સંપાતનું ખસવું- વાત આપણે આવતા લેખમાં કરીશું. ઉપરાંત આકાશી પદાર્થ પૃથ્વી પરના કોઇ સ્થળ પરથી જોતાં તે કઇ દિશામાં અને આકાશમાં, ક્ષિતિજથી કેટલો ઉપર દેખાશે તે જાણવા માટે પદાર્થના વિષુવવૃત્તિય યામને સ્થાનિક યામની પદ્ધતિમાં બદલવા જરૂરી છે. આવતા લેખમાં આપણે આ પદ્ધતિ વિષે પણ વાત કરીશું.
વાચક મિત્રોની ટિપ્પણી અને સૂચન હંમેશ માફક આવકાર્ય છે