લેખક : રાજેન્દ્ર દવે / સી એમ નાગરાણી
ચંદ્રયાન અને આદિત્ય L1 વિષેના લેખમાં અલગ-અલગ પ્રકારની કક્ષા (Orbit- ઓરબીટ) નો ઉલ્લેખ વારંવાર થયો હતો. ભવિષ્યમાં પણ આ વેબસાઇટ પર “કક્ષા” સાથે આપણી મુલાકાત અવારનવાર થતી રહેશે, કારણ કે ખગોળશાસ્ત્ર તેમજ અંતરિક્ષ સંશોધન ક્ષેત્રમાં કક્ષાની સંકલ્પના, અને એની સમજણ, ખૂબ જ મહત્વની છે. માટે અમારો વિચાર આ લેખમાં કક્ષા વિષે વિગતે ચર્ચા કરી લેવાનો છે, જેથી ખગોળશાસ્ત્ર અને અંતરિક્ષ-સંશોધન વિષેના લેખ સરળતાથી સમજી શકાય.
માની લો કે કોઇ ઊંચી ટેકરીની ટોચ પર એક તોપ ગોઠવી છે. આ તોપનો ગોળો જો સમ-ક્ષિતિજ (Horizontal – હોરીઝોન્ટલ) દિશામાં છોડવામાં આવે તો એ પોતાની સમ-ક્ષિતિજ ગતિ અને પૃથ્વીના ગુરુત્વાકર્ષણની સંયુક્ત અસર નીચે, વણાંક વાળા પથ પર ગતિ કરતો જમીન પર પડશે. ગોળાના પથનો વણાંક (curvature- કર્વેચર) ગોળાની શરૂઆતની ગતિ પર આધારિત છે. જેમ ગતિ વધુ, એમ પથનો વણાંક ઓછો, અને ગોળો જ્યાં જમીન પર પડે એ સ્થાનનું તોપથી અંતર વધુ. પરંતુ પૃથ્વી પોતે ગોળ છે. તેથી જો આપણે ગોળાની ગતિ વધારતા જઈએ, તો એક સમયે ગોળાના પથનો વણાંક પૃથ્વીના વણાંક જેટલો થઇ જાય. આવી સ્થિતિમાં ગોળો સતત “પડ્યા” તો કરે, પરંતુ ક્યારે પણ જમીનને અડે નહીં, અને પૃથ્વીના ગુરુત્વાકર્ષણ સિવાયના કોઇ બળની મદદ વિના, સતત પૃથ્વીની આસપાસ ફરતો રહે! બસ, આપણો ગોળો કક્ષામાં પહોંચી, કૃત્રિમ ઉપગ્રહ બની ગયો! અલબત્ત, થોડા સમયમાં વાતાવરણ સાથેના ઘર્ષણને કારણે ગોળાની ગતિ ઓછી થઇ જાય, અને એના પથનો વણાંક વધી જતા, એ છેવટે જમીન પડે. પરંતુ, જો ટેકરી એટલી ઊંચી હોય કે એની ટોચ વાતાવરણની બહાર નીકળતી હોય, જ્યાં વાતાવરણ સાથેનું ઘર્ષણ નગણ્ય હોય, તો આપણો ઉપગ્રહ કોઇ પણ ઊર્જા વાપર્યા વગર, પોતાની કક્ષામાં પૃથ્વીના કેન્દ્રની આસપાસ ભ્રમણ કરતો રહેશે (અલબત્ત, પૃથ્વીનું એક પરિભ્રમણ કરી ઉપગ્રહ ટેકરીની સાથે અથડાય એ પહેલાં આપણે ટેકરીને એના પથમાંથી ખસેડી જરૂર લેવી પડે!). ઉપરના વિવરણને સરળ બનાવવા અમેં ધારી લીધું કે પૃથ્વીના વજનની સરખામણીમાં ઉપગ્રહનું વજન નગણ્ય છે. લેખમાં આગળ, આપણે જ્યાં આવી ધારણા અયોગ્ય હોય એવી સ્થિતી, એવા ઉદાહરણની પણ ચર્ચા કરીશું.

આમ તો “કક્ષા”ના ખ્યાલની સમજ કેન્દ્રગામી (Centripetal- સેન્ટ્રીપીટલ) અને કેન્દ્રત્યાગી (Centrifugal- સેન્ટ્રીફ્યુગલ) જેવા આભાસી બળથી માંડી આઇન્સ્ટાઇનની જનરલ રીલેટીવીટી (General Relativity) જેવા વિવિધ સિદ્ધાંત દ્વારા આપી શકાય. પરંતુ ઉપર દર્શાવેલ વિવરણ, સાદી, સરળ, કોઇ પણ ગણિત અને સમીકરણ વગરની રીત છે. થોડી અચોક્કસ ખરી, પણ પ્રાથમિક સમજ માટે પર્યાપ્ત છે.
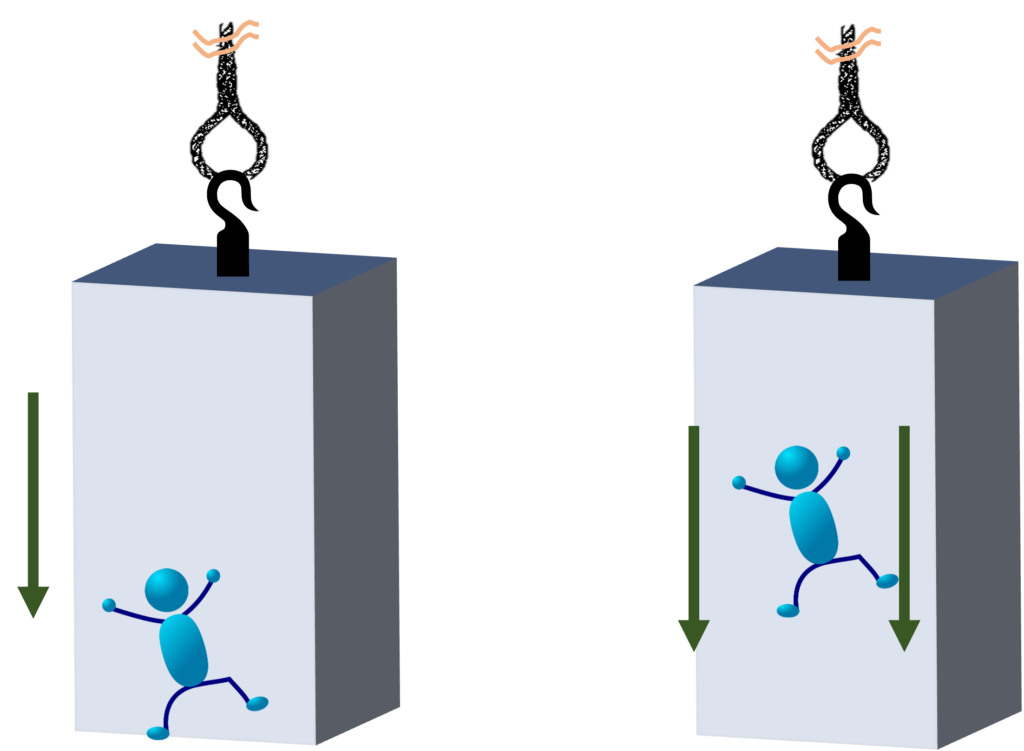
કક્ષા વિષેની આવી સમજણ, એક વ્યાપક ગેરસમજને દૂર કરવા માટે પણ ઉપયોગી છે. સામાન્ય માન્યતા પ્રમાણે યાન પૃથ્વીની કક્ષામાં પહોંચે, ત્યારે તે પૃથ્વીના ગુરૂત્વાકર્ષણની બહાર નિકળી જાય છે અને તેથી અંતરિક્ષ-યાનમાં યાત્રી વજન-વિહીનતાનો અનુભવ કરે છે, તેઓ પોતે અને તેમની આસપાસની છૂટી રાખેલી ચીજ-વસ્તુ જાણે યાનમાં તરતી હોય એમ ફરતી રહે છે. ખરેખર તો યાન પોતે પૃથ્વીના ગુરૂત્વાકર્ષણને કારણે જ કક્ષામાં ફરતું રહે છે. એ સતત પૃથ્વીના ગુરૂત્વાકર્ષણની અસર હેઠળ હોય છે. તેથી, કક્ષામાં વજન-વિહીનતાના અનુભવ માટે ગુરૂત્વાકર્ષણનો અભાવ જવાબદાર નથી.
કક્ષામાં વજન-વિહીનતાને સમજવા માટે, “વજન” એટલે શું એ સમજવું જરૂરી છે. પૃથ્વી પર આપણે જેના પર ઊભા રહીએ એ ભોંય, ગુરૂત્વાકર્ષણનો સામનો કરી એક પ્રતિઘાત (reaction -રીએક્શન) બળ વડે આપણને ટેકો આપે છે, આપણે જાણે જમીનને દબાવતા હોઇએ એવો અનુભવ થાય છે. આ બળ, આ અનુભવ જ, “વજન” છે. આવા ટેકા વગર આપણે વજન વિહીન બની જઇએ! જો કોઇ ઊંચા મકાનના સૌથી ઉપરના માળે ઉભેલી લિફ્ટનું દોરડું કપાઇ જાય અને એ જમીન તરફ પડવા લાગે, તો એમાં ઉભેલી વ્યક્તિને પણ વજન-વિહીનતાનો જ અનુભવ થાય. એ જો લિફ્ટમાં કુદે, તો લિફ્ટની ભોંયથી અધ્ધર જ રહી જાય! આપણે જોયું એ પ્રમાણે, કક્ષામાં ફરતું યાન, જમીનને ક્યારેય અડ્યા વગર પૃથ્વી તરફ સતત “પડતું” રહે છે, એ પોતે, અને એમાં રહેલી દરેક ચીજનો- યાત્રી સહીત- પ્રવેગ તેમજ ગતિ એક સરખી રહે છે. યાત્રી જે ખુરશી પર બેઠા હોય તે ખુરશી, જેના પર ચાલવાની કોશિશ કરે તે ભોંય સહિત બધા જ, ગુરૂત્વાકર્ષણની અસર હેઠળ એક સરખી ગતિથી પૃથ્વી તરફ પડતાં રહે છે. સતત “પડતા” રહેતા અંતરિક્ષયાનની સ્થિતી પણ ભોંય તરફ પડતી લિફ્ટ જેવી જ છે. માટે, કક્ષામાં ફરતા અંતરિક્ષયાનમાં વજન-વિહીનતા માટે, ગુરૂત્વાકર્ષણનો અભાવ નહીં, પણ ગુરૂત્વાકર્ષણની અસર નીચે યાનનું સતત “પડતા” રહેવું જવાબદાર છે.
આ તો એક આડ-વાત થઇ, હવે આપણે મૂળ વાત પર આવીએ. આપણે જોયું કે તોપમાં ગોળાના પથનો વળાંક તેની સમ-ક્ષિતિજ ગતિ પર આધાર રાખે છે, વળી, આ વણાંક જ્યારે પૃથ્વીની સપાટીના વણાંક જેટલો – એક વર્તુળ જેટલો- થાય, ત્યારે ગોળો પૃથ્વીની આસપાસ, માત્ર પૃથ્વીના ગુરુત્વાકર્ષણ ની અસર નીચે વર્તુળાકાર કક્ષામાં ફર્યા કરે છે. વર્તુળાકાર કક્ષા માટે કેટલી સમ-ક્ષિતિજ ગતિની જરૂર પડે, એનો આધાર જે તે સ્થાન પરના ગુરૂત્વાકર્ષણ પર છે- ગુરૂત્વાકર્ષણ જેટલું વધારે, વર્તુળાકાર કક્ષા માટે ગતિની જરૂર પણ એટલી વધારે. પૃથ્વીની સપાટી પર તો વાતાવરણ સાથેના ઘર્ષણને કારણે કક્ષા સંભવ નથી, પરંતુ સપાટીથી આશરે 400 કિ.મી. ઊંચે વર્તુળાકાર કક્ષામાં ઘુમતા આંતરરાષ્ટ્રીય સ્પેસ સ્ટેશનને કક્ષામાં રહેવા આશરે 7.66 કિ.મી/સેકન્ડ ની ગતિની જરૂર પડે છે. ન્યુટનના ગુરૂત્વાકર્ષણના નિયમ અનુસાર બે પદાર્થ વચ્ચેનું અંતર વધારતા બન્ને વચ્ચેનું ગુરૂત્વાકર્ષણ ઘટતું જાય. તેથી, પૃથ્વીની સપાટીથી 36,000 કિ.મી ઊંચેની કક્ષામાં ઘુમતા સંદેશ-વહેવાર માટેના ઉપગ્રહને માત્ર 3.07 કિ.મી./સેકન્ડ ગતિની જરૂર પડે. ચંદ્રનું ગુરૂત્વાકર્ષણ પૃથ્વીના ગુરૂત્વાકર્ષણ કરતા ઘણું ઓછું છે. તેથી ચંદ્રની સપાટીથી ઉપર 100 કિ.મી જેટલી નીચી કક્ષામાં ઘુમતા ચંદ્રયાન ઓરબીટરને પણ માત્ર 1.6 કિ.મી/સેકન્ડ ની ગતિ જોઇએ. બીજી તરફ, સૂ્ર્યના શક્તિશાળી ગુરૂત્વાકર્ષણની અસર નીચે, તેની આસપાસ 1,50,00,000 કિ.મી. જેટલે દૂર રહીને ફરતી પૃથ્વીને પણ કક્ષામાં ટકી રહેવા સારુ દરેક સેકન્ડે 30 કિ.મી. ની ઝડપે ફરવું પડે છે!

ઉપરની ચર્ચા પરથી આપણને યાનને વર્તુળાકાર કક્ષામાં મુકવાની રીત મળી. યાનને જેટલી ઊંચાઈની કક્ષા મૂકવું હોય એટલે ઊંચે લઇ જવાનું, અને ત્યાં પહોંચી, એને ધક્કો મારી વર્તુળાકાર કક્ષા માટે જરૂરી સમ-ક્ષિતિજ ગતિ આપી દેવાની. બસ, કામ પૂરું! એક સ્વાભાવિક પ્રશ્ન ઊઠે. જો યાનને મળેલી સમ-ક્ષિતિજ ગતિ વર્તુળાકાર કક્ષા માટે જરૂરી ગતિથી ઓછી, અથવા વધારે હોય તો શું થાય? કમનસીબે, આવી સ્થિતીમાં ઉપર જણાવેલી સરળ સમજથી કામ ચલાવવું મુશ્કેલ છે. એના માટે આપણે ગુરૂત્વાકર્ષણ ઉપરાંત ઊર્જા (Energy-એનર્જી) અને ર્કોણીય વેગમાન (Angular Momentum- એનગ્યુલર મોમેન્ટમ) ના સંરક્ષણ (conservation -કન્ઝર્વેશન)ના નિયમનો ઉપયોગ કરવો રહ્યો.
યાનને મળેલી સમ-ક્ષિતિજ (બીજા શબ્દોમાં, યાનને પૃથ્વી સાથે જોડતી રેખાને લંબ દિશામાં) ગતિ જો વર્તુળાકાર કક્ષા માટે જરૂરી ગતિથી ઓછી હોય, તો આપણે ઉપર જોયું એ પ્રમાણે યાનના પથનો વળાંક વર્તુળાકાર વળાંક કરતા વધુ રહે. યાનની ગતિ જો જરૂરી ગતિ કરતા ઘણી ઓછી હોય, તો પથનો વળાંક ખૂબ વધુ રહે, અને શક્ય છે કે યાન પૃથ્વી સાથે અથડાય (સીમાંત કિસ્સામાં યાનને કોઇ સમ-ક્ષિતિજ ગતિ આપ્યા વિના, બસ ઊંચાઈ પર લઇ જઇ છોડી દેવામાં આવે તો અલબત, એ સીધું જ જમીન પર પડે!). યાનની ગતિ પૃથ્વી સાથે અથડમણ થાય એટલી ઓછી ન હોય, તો પણ પથના વધુ પડતા વળાંકને કારણે યાનનું પૃથ્વીથી અંતર ઘટતું જાય. પરિણામે, કોણીય-વેગમાનના સંરક્ષણના નિયમ અનુસાર યાનની સમ-ક્ષિતિજ ગતિ વધતી જાય. પરંતુ હવે વધારાની ગતિને કારણે યાનના પથનો વળાંક વર્તુળાકાર કક્ષાના વળાંકથી ઓછો થઇ જાય, યાન પૃથ્વીથી દૂર જવા લાગે, અને યાન ફરી પથના શરૂઆતના બિંદુએ પહોંચે ત્યાં સુધી તેની ગતિ ઘટતી રહે.
આવા પથમાં ભ્રમણ કરતા યાનમાં બે પ્રકારની ઊર્જા રહેલી હોય, એક તો યાનના સ્થાન પર પૃથ્વીના ગરૂત્વાકર્ષણ ક્ષેત્રને કારણે ઉદ્દભવતી ઊર્જા. આ ઊર્જા, જે-તે સમયે યાનની પૃથ્વીથી ઊંચાઈ પર આધાર રાખે છે. જેમ યાનની ઊંચાઈ વધારે, એમ ઊર્જા વધારે. આવી, સ્થાન પર આધારિત ઊર્જાને “પોટેન્શિયલ” ઊર્જા (Potential Energy – પોટેન્શિયલ એનર્જી) કહે છે. યાન પોતાની ની ગતિને કારણે જે ઊર્જા ધરાવે છે એ ગતિશક્તિ (Kinetic Energy – કાયનેટિક એનર્જી), યાનની બીજા પ્રકારની ઊર્જા છે. યાનના પથ દરમ્યાન એની ઊંચાઈ તેમજ ગતિમાં થતા ફેરફારને પરિણામે એની પોટેન્શિયલ અને કાયનેટિક ઊર્જા બદલાતી રહે છે, પરંતુ ઊર્જા સંરક્ષણના નિયમ અનુસાર આખા પથમાં યાનની બન્ને પ્રકારની ઊર્જાનો સરવાળો અચળ રહે છે. માટે, યાનની ગતિ જ્યારે સૌથી વધારે હોય, ત્યારે કક્ષામાં તેની કાયનેટિક ઊર્જા મહત્તમ હોય અને પોટેન્શિયલ ઊર્જા સૌથી ઓછી, ન્યૂનતમ હોય. અર્થાત્, તે સમયે યાન પૃથ્વીની સૌથી નજીક હોય. કક્ષાના આવા, પૃથ્વીથી સૌથી નજીકના બિંદુને કક્ષાનું “પેરીજી” (Perigee) બિંદુ કહે છે. બીજી તરફ, જ્યારે યાનની ગતિ કક્ષામાં સૌથી ઓછી હોય, ત્યારે એની કાયનેટિક ઊર્જા ન્યૂનતમ અને પોટેન્શિયલ ઊર્જા મહત્તમ હોય. અર્થાત્ યાન પૃથ્વીથી સૌથી દૂર હોય. આવા, પૃથ્વીથી સૌથી દૂરના બિંદુને કક્ષાનું “એપોજી” (Apogee) બિંદુ કહે છે (ગ્રીક ભાષામાં peri-પેરી નજીક, apo-એપો દૂર અને gee-જી પૃથ્વી દર્શાવે છે. અલબત્ત, યાન જો પૃથ્વી સિવાયના પિંડની કક્ષામાં ફરતું હોય તો એની કક્ષાના આવા બિંદુના નામ અલગ હોય. ઉદાહરણ રૂપે, સૂર્યની કક્ષામાં આ બિંદુઓ અનુક્રમે પેરીહિલીઓન (Perihelion) અને એપહિલીઓન (Aphelion) તરીકે ઓળખાય છે.). કક્ષાના એપોજી તથા પેરીજી બિંદુ પૃથ્વીથી અલગ-અલગ અંતર પર આવેલા હોવાથી આવી કક્ષાનો આકાર દીર્ધ-વર્તુળ, લંબગોળ હોય છે. આવી જ ચર્ચા ઉલટા કિસ્સા- જ્યાં યાનની સમ-ક્ષિતિજ ગતિ વર્તુળાકાર કક્ષા માટે જરૂરી ગતિથી વધુ હોય- માટે પણ કરી શકાય. આવી સ્થિતિમાં પણ યાનની કક્ષાનો આકાર દીર્ધ-વર્તુળ જ હશે.

ઉપરની ચર્ચા માત્ર પૃથ્વીની આસપાસ ભ્રમણ કરતા યાનની સુધી સીમિત નથી, પણ એક ઉલ્કા જેવા નાના ખગોળીય પિંડની આસપાસ ભ્રમણ કરતી બીજી ઉલ્કાથી શરુ કરી આકાશગંગા જેવા વિશાળ પિંડની આસપાસ ભ્રમણ કરતા તારા માટે પણ એ એટલી જ લાગુ પડે છે.
લેખના આ, પહેલા ભાગમાં આપણે કક્ષાને સરળ રૂપે સમજવા પ્રયત્ન કર્યો. હવે પછીના ભાગમાં આ વિષયે વધુ વિસ્તાર તેમજ ઊંડણથી ચર્ચા કરીશું. દરમ્યાન, હંમેશ મુજબ, લેખ વિષે સૂચન અને ટિપ્પણીનું સ્વાગત છે.