ચંદ્ર, સૂર્ય અને સમુદ્રમાં ભરતી

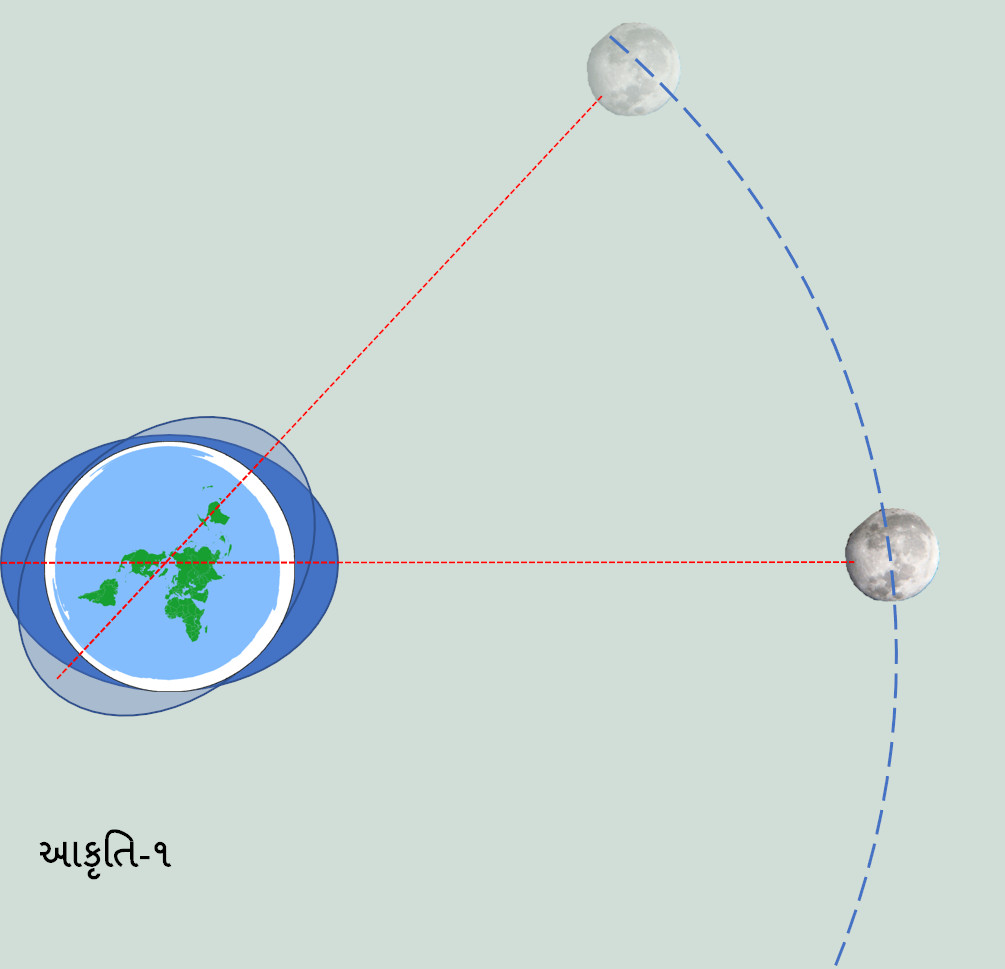
પૃથ્વીના સમુદ્રમાં આવતા ભરતી તથા ઓટનો વિષય દેખાય છે તેટલો સરળ નથી. આપણે બધા શાળામાં શીખી ચૂક્યા છીએ તે પ્રમાણે સમુદ્રમાં ભરતી દિવસમાં આશરે બે વખત આવે છે. જ્યારે ચંદ્ર માથા પર હોય ત્યારે અને ઉપરાંત જ્યારે તે પૃથ્વીની સામી બાજુ હોય ત્યારે. માનો સમુદ્રનું પાણી પૃથ્વીની ફરતું એક લંબગોળ બનાવે છે, જેની લાંબી ધરી હંમેશા ચંદ્ર તરફ રહે છે (આકૃતિ -૧). સાથે-સાથે આપણને એ પણ શીખવવામાં આવ્યું છે કે ભરતીનું કારણ ચંદ્ર  (તથા ઓછા અંશે, સૂર્ય) નું ગુરૂત્વાકર્ષણ બળ છે. પરંતુ દિવસની બીજી ભરતીમાં તો સમુદ્રનું પાણી ચંદ્રથી દૂર જાય છે! આવું શી રીતે બની શકે? ચંદ્રથી દૂરની બાજુ પર આવતી ભરતી ઘણી ગૂંચવણ ઊભી કરે છે. ગૂંચવણનું બીજું કારણ સૂર્ય છે. બધા જાણે છે કે સૂર્યનું ગુરૂત્વાકર્ષણ ચંદ્ર કરતા ઘણું વધારે બળવાન છે. તો પછી ભરતીનું મુખ્ય કારણ ચંદ્ર શા માટે? સૂર્ય શા માટે નહીં?

આપણા એક વાચક મિત્રે ઇ-મેઇલ મોકલી આ ગૂંચવણને વાચા આપી છે. તેમણે પોતાનું નામ-સરનામું તો દર્શાવ્યું નથી પરંતુ આ લેખ પૂરતું આપણે માની લઇએ કે તેમનું નામ મોહિતભાઇ છે! મોહિતભાઇએ મોકલેલું લખાણ બાજુમાં બતાવ્યું છે. લખાણના મુખ્ય તારણ નીચે મુજબ છે

૧) ભરતીનું કારણ પૃથ્વીની બે બાજુ પર લાગતાં ગુરૂત્વાકર્પણ બળની અસમાનતા છે.

૨) ભરતીનું  કારણ સૂર્ય છે, ચંદ્ર નહીં.

૩) સૂર્યના ગુરૂત્વાકર્ષણ બળને કારણે પૃથ્વી પર રહેલા પદાર્થના વજનમાં ફેરફાર થાય છે.

ચાલો, મોહિતભાઇએ ઊભા કરેલ મુદ્દાની ચર્ચા કરીએ.  પ્રશ્નને સરળ રાખવા આપણે પૃથ્વીના ભ્રમણને કારણે ઉત્પન્ન થતી ગૌણ અસરની અવગણના કરી માત્ર ગુરૂત્વાકર્ષણ બળ પર આપણું ધ્યાન કેન્દ્રિત કરીશું. આગળ વધતાં પહેલા એક વાતની ચોખવટ કરી લઇએ. હું ભૌતિકશાસ્ત્રી નથી, મારું ભૌતિકશાસ્ત્ર વિષેનું જ્ઞાન સીમિત છે. ઉપરાંત આ ચર્ચામાં મારો ભાર સરળતા તરફ વધારે અને ચોકસાઈ (rigor- રીગર)  તરફ ઓછો રહેશે. તેથી શક્ય છે કે ચર્ચામાં કોઇ હકીકત-દોષ રહી જાય. વાચક-મિત્રો તરફથી સૂચન અને સુધારા હંમેશ મુજબ આવકાર્ય  છે.

શરૂઆત આપણે પૃથ્વી પર ચંદ્રના ગુરૂત્વાકર્ષણ બળના અંદાજથી કરીશું. આ માટે આપણે એક-એક કિલોગ્રામ દળ (mass- માસ)ના ત્રણ દડા વાપરીશું. પહેલો દડો (A) આપણે પૃથ્વીની સપાટી પર, ચંદ્રની બિલકુલ નીચે, અર્થાત્ ચંદ્ર તથા પૃથ્વીના કેન્દ્રને જોડતી રેખા પૃથ્વીની સપાટીને જ્યાં છેદે, ત્યાં રાખેલો છે. બીજો દડો પૃથ્વીની સપાટી પર, પહેલા દડાની સામેની બાજુ (B)  રાખેલો છે અને ત્રીજો દડો (C) પૃથ્વી ના કેન્દ્ર પર રાખેલો છે. આ ત્રણે દડા પર ચંદ્રના ગુરૂત્વાકર્ષણને કારણે કેટલું બળ લાગશે તે આપણે ન્યુટનના ગુરૂત્વાકર્ષણના નિયમની મદદથી શોધી શકીએ. ચંદ્રનું દળ (mass- માસ)   7.35 X 10²² કિલોગ્રામ, ચંદ્રના કેન્દ્ર અને પૃથ્વીના કેન્દ્ર વચ્ચેનું અંતર 3,84,000 કિલોમીટર તથા પૃથ્વીની ત્રિજ્યા 6,370  કિલોમીટર લેતાં દડા (A), (B)  અને (C) પર ચંદ્રના ગુરૂત્વાકર્ષણને કારણે લાગતું બળ અનુક્રમે 3.4316X 10^-05 ન્યુટન, 3.2114X10^-05  ન્યુટન, અને 3.3187X 10^-05   ન્યુટન  જેટલું હશે (1 ન્યુટન બરાબર એટલું બળ, જે  1 કિલોગ્રામ દળના પદાર્થને 1 મીટર/સેકન્ડ^૨ જેટલો પ્રવેગ (acceleration- એક્સલરેશન) આપે). આ ત્રણે બળને આકૃતિ -૨(a) માં દર્શાવ્યા છે.

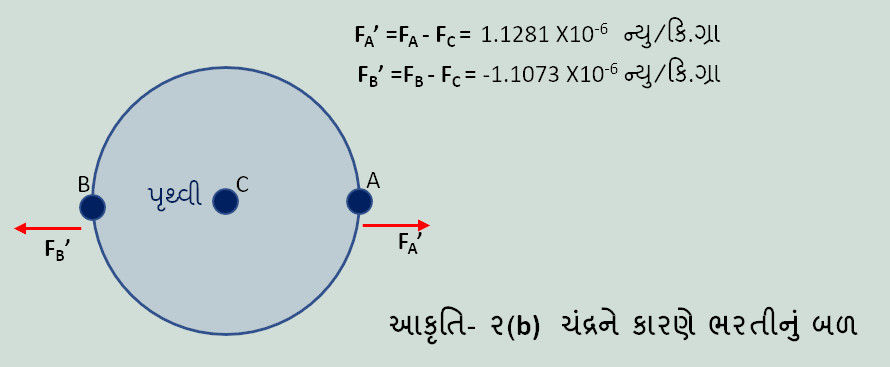
બીજું પગથિયું આપણે ગણી કાઢેલા બળની સમુદ્રના પાણી પર થતી અસર, ખાસ કરીને ભરતીને લગતી અસર તપાસવાનું છે. આપણે જાણીએ છીએ કે ભરતી તથા ઓટ સમુદ્રના પાણીની સપાટીમાં ફેરફાર, તેના પૃથ્વીના કેન્દ્રથી અંતરમાં ફેરફાર બતાવે છે. તેથી તેમને સમજવા માટે સમુદ્રના પાણી પર પૃથ્વીના કેન્દ્રની સાપેક્ષમાં લાગતાં બળને સમજવું જરૂરી છે. બીજી રીતે કહીએ ભરતીને સમજવા માટે આપણે દડા (A) અને (B) પર પૃથ્વીના કેન્દ્રની સાપેક્ષમાં લાગતાં બળ શોધી કાઢવા જોઇએ. તે માટે આકૃતિ -૨(a)ના બધા બળમાંથી કેન્દ્રમાં રહેલા દડા (C) પર લાગતાં બળની બાદબાકી કરવી પડે. બાદબાકી પછી બચેલા બળ આકૃતિ -૨(b)માં બતાવ્યા છે. દડા (C) પરનું બળ તો શૂન્ય થઇ ગયું જ્યારે દડા (A) પર +1.129 X10^-6 ન્યુટન અને દડા (B) પર -1.1073 X10^-6   ન્યુટન જેટલું બળ (પૃથ્વીના કેન્દ્રની સાપેક્ષમાં)  લાગશે. પરંતુ બળ એક દેશિક (vector- વેક્ટર) છે. તેથી દડા (B) પરના બળની ઋણ સંજ્ઞાનો અર્થ બળની ઊલટી દિશા થાય.. આકૃતિ મુજબ પૃથ્વીના કેન્દ્રની સાપેક્ષમાં જોતાં ચંદ્રના ગુરૂત્વાકર્ષણનું બળ પૃથ્વીની ચંદ્ર તરફની સપાટી તથા તેનાથી ઊલટી બાજુની, એમ બન્ને સપાટી પર  કેન્દ્રથી વિરુદ્ધ દિશામાં લાગે છે. આ એક આશ્ચર્યજનક  હકીકત  છે અને સમુદ્રમાં ભરતી ચંદ્ર તરફ તથા તેની વિરુદ્ધ તેમ બેઉ તરફ એક સાથે આવે છે તે ઘટનાને સમજવાની આ એક રીત છે. બીજી રીતે કહીએ તો ચંદ્રનું ગુરૂત્વાકર્ષણ બળ પૃથ્વીની ચંદ્ર તરફની સપાટી પર સૌથી વધુ લાગે છે. તેનાથી ઓછું પૃથ્વીના કેન્દ્ર પર અને સૌથી ઓછું જે સપાટી ચંદ્રની વિરુદ્ધ બાજુ છે તેના પર લાગે છે. તેને કારણે સમુદ્રનું પાણી બેઉ બાજુ કેન્દ્રથી દૂર જાય છે, સમુદ્રની સપાટી ઊંચી જાય છે.    

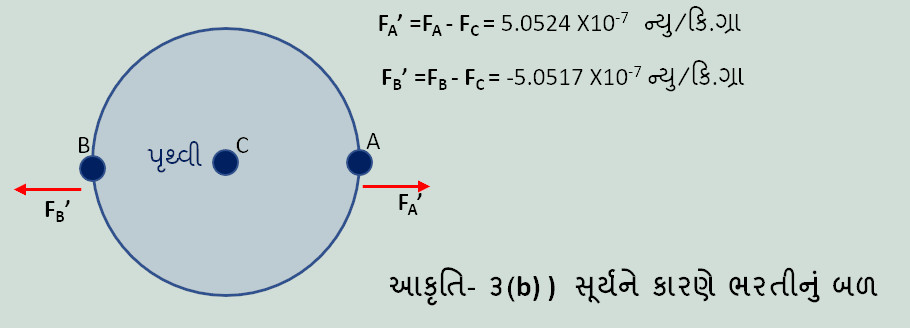
આવી જ ગણતરી સૂર્ય (દળઃ 1.989X10³⁰ કિલોગ્રામ અને  અંતરઃ 1.496X10⁸ કિલોમીટર) ના ગુરૂત્વાકર્ષણને કારણે પૃથ્વી પર લાગતાં બળ માટે  આકૃતિ-૩માં દર્શાવી છે. આકૃતિ-૩(a) બતાવે છે કે ચંદ્રની સરખામણીમાં સૂર્યના ગુરૂત્વાકર્ષણના કારણે લાગતું બળ ઘણું વધારે, લગભગ 180 ગણું છે (તેમાં આશ્ચર્ય શું?) પરંતુ સાથે-સાથે તે  વધુ એકરૂપ, એકસમાન છે. પૃથ્વી પર જુદી-જુદી જગાએ સૂર્યના ગુરૂત્વાકર્ષણના કારણે લાગતાં બળમાં ઝાઝો ફેરફાર નથી. હકીકતમાં આકૃતિ ૩(b)માં  દર્શાવ્યા મુજબ આ ફેરફાર ચંદ્રની સરખામણીમાં લગભગ અડધો છે. આમ થવાનું કારણ પૃથ્વીની ત્રિજ્યાની સરખામણીમાં  સૂર્ય અને ચંદ્રનું પૃથ્વીથી અંતર છે. પૃથ્વીની ત્રિજ્યા સૂર્યથી પૃથ્વીના અંતરના માત્ર 0.004% છે. આ સામે પૃથ્વીની ત્રિજ્યા ચંદ્રથી પૃથ્વીના અંતરના ખાસ્સા 1.66% છે. આ ફરકના કારણે પૃથ્વી પર સૂર્યનું ગુરૂત્વાકર્ષણનું બળ ચંદ્રના ગુરૂત્વાકર્ષણ બળ કરતાં લગભગ 180 ગણું  હોવા છતાં સમુદ્રમાં ભરતી પર ચંદ્રની અસર સૂર્યની અસર કરતાં બે ગણીથી વધારે છે. આમ, ભરતીનું મુખ્ય કારણ ચંદ્ર છે, પરંતુ સાથે-સાથે સૂર્યની અસર પણ નગણ્ય નથી. તેથી જ પૂનમ અને અમાસ ના દિવસે, જ્યારે સૂર્ય અને ચંદ્ર લગભગ એક રેખા પર હોય છે ત્યારે, તેમની અસર એકબીજાને મદદ કરે છે અને સમુદ્રમાં મોટી ભરતી લાવે છે!

સુધારો (તારીખ ૧ મે, ૨૦૧૯)- ઉપરની આકૃતિમાં F_c  ની કિંમત 5.931479X10^-05  નહીં, 5.931479X10^-0૩ હોવી જોઇએ.

આ સાથે મારા મત પ્રમાણે આપણે મોહિતભાઈના પહેલા બે મુદ્દાનું સમાધાન કરી દીધું છે. સમુદ્રમાં ભરતીનું મુખ્ય કારણ અસમાન ગુરૂત્વાકર્ષણ છે, તે સાચું, પરંતુ તેની પાછળનું ભૌતિકશાસ્ત્ર મોહિતભાઇની માન્યતા કરતાં થોડું જુદું છે. વળી ભરતી પર સૂર્યની અસર છે તે પણ સાચું, પરંતુ ભરતી પર ચંદ્રની અસર સૂર્યની અસર  કરતા લગભગ બે ગણી છે. હવે બાકી રહે છે તેમનો છેલ્લો મુદ્દો, સૂર્યના ગુરત્વાકર્ષણની પૃથ્વી પરના પદાર્થના વજન પર અસર.

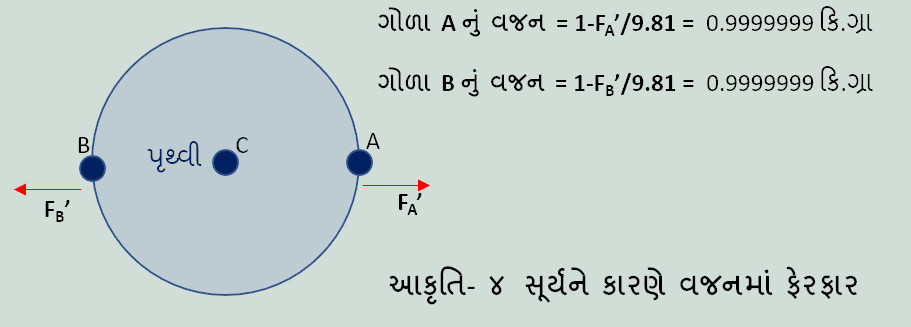
ઔપચારિક વ્યાખ્યા મુજબ પદાર્થનું પૃથ્વી પર વજન તેના પર, પૃથ્વીના કેન્દ્રની દિશામાં લાગતાં, પૃથ્વીના ગુરૂત્વાકર્ષણ બળ બરોબર હોય. દેખીતી રીતે આ બળ પદાર્થના દળના પણ સપ્રમાણમાં હોય છે. પૃથ્વીની સપાટી પર એક કિલોગ્રામ દળના પદાર્થ પર 9.81 ન્યુટન બળ લાગે છે. હવે, પરંપરા અનુસાર આ 9.81 ન્યુટન બળને એક કિલોગ્રામ બળ કહે છે. અર્થાત્ એક કિલોગ્રામ “દળ”ના પદાર્થ પર પૃથ્વીની સપાટી પર પૃથ્વીના ગુરૂત્વાકર્ષણને કારણે એક કિલોગ્રામ “બળ” લાગે અને તે પદાર્થનું “વજન” એક કિલોગ્રામ કહેવાય.  બીજા શબ્દોમાં જેના પર એક કિલોગ્રામ (9.81 ન્યુટન) બળ લાગતું હોય તે પદાર્થનું વજન એક કિલોગ્રામ હોય. આમ “કિલોગ્રામ” તે દળ, બળ (અને વજન) તેમ બન્નેનો એકમ છે. હવે ઘણા કારણ સર પદાર્થ પર ગરૂત્વાકર્ષણ સિવાયના બળ લાગે છે અને તેથી તેનું દેખીતું, અર્થાત્ apparent- એપેરન્ટ વજન તેના સાચા વજનથી જુદું પડે છે, ઉદાહરણ રૂપે પદાર્થને પ્રવાહીમાં મૂકતાં પ્રવાહીની તારક-શક્તિ (buoyancy – બોયન્સી)નું બળ ગુરૂત્વાકર્ષણની સામે કામ કરે છે અને પદાર્થનું દેખીતું વજન ઘટે છે. તેવી જ રીતે કોઇ ચુંબકીય પદાર્થનું દેખીતું વજન તેની નીચે ચુંબક રાખીને વધારી શકાય (આવા છેતરામણા ત્રાજવાથી કોણ છેતરાયું નથી?). શું પ્રવાહીની તારક-શક્તિની માફક સૂર્ય (તથા ચંદ્ર) ના  ગુરૂત્વાકર્ષણ બળને કારણે  પદાર્થનું  દેખીતું વજન બદલાઈ શકે? આકૃતિ-૩(b)ના F_A’ અને F_B’ માં   જો આપણે પૃથ્વીના ગુરૂત્વાકર્ષણને કારણે  લાગતું બળ (9.81 ન્યુટન/કિલોગ્રામ) ઉમેરીએ તો પરિણામે પૃથ્વીના કેન્દ્ર તરફ જે બળ મળે તે પરથી  પદાર્થનું દેખીતું વજન શોધી શકાય( આકૃત્તિ-૪).  આકૃતિમાં દર્શાવ્યા અનુસાર સૂર્યના ગુરૂત્વાકર્ષણને કારણે પૃથ્વીની બન્ને બાજુ પદાર્થનું વજન ઓછું થાય છે! અલબત આ ઘટાડો સાવ નાનો છે, એક કિલોગ્રામ વજનમાં એક મિલીગ્રામથી પણ ઓછો. આવી જ રીતે ચંદ્રના ગુરૂત્વાકર્ષણને કારણે પણ દેખીતા વજનમાં ઘટાડો જોવા મળે છે (અલબત, સૂર્યની સરખામણીમાં બમણો!). એક રીતે જોઇએ તો વજનમાં થતો ઘટાડો જ સમુદ્રની ભરતી માટે જવાબદાર છે! આમ મોહિતભાઇનું ત્રીજું તારણ પણ ખોટું નથી, ફરક માત્ર દિશાનો છે!

આ હતી સમુદ્રની ભરતી બાબતમાં મારી સમજ. આશા છે કે મારી આ લાંબી વાર્તાના અંતે આ બાબતની ગૂંચવણ થોડી ઓછી થઇ હશે, કમ-સે-કમ વધી તો નહીં જ હોય!